4D Rotation Matrix - Graph 4D

This program rotates points about the XY, YZ, XZ, XU, YU, and ZU axises. I then projects each 4D vector to the 2D canvas. The Jar file can be downloaded here: Graph4D.jar

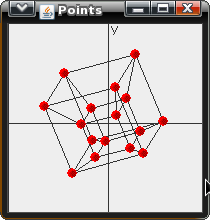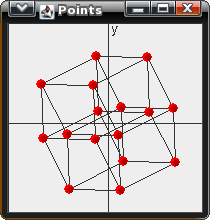Before looking at the source, let's take a look at some of the fundamental mathematics behind the software. If you are uncomfortable with the thought of 4D matrix rotations, then I recommend reading Wikipedia, or checking out my article about 3D graphing, which can be found here. In this example, I will only show the 4D rotation matrices. Note that for each rotation matrix, 2 axises are held still while the vector is rotated around the other two axises. This may be hard to visualize at first, but It will become clear after a while.

$$ rotXY = \left[\begin{matrix} cos(\theta) & sin(\theta) & 0 & 0 \\ -sin(\theta) & cos(\theta) & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \end{matrix}\right] $$

$$ rotYZ = \left[\begin{matrix} 1 & 0 & 0 & 0 \\ 0 & cos(\theta) & sin(\theta) & 0 \\ 0 & -sin(\theta) & cos(\theta) & 0 \\ 0 & 0 & 0 & 1 \end{matrix}\right] $$

$$ rotXZ = \left[\begin{matrix} cos(\theta) & 0 & -sin(\theta) & 0 \\ 0 & 1 & 0 & 0 \\ sin(\theta) & 0 & cos(\theta) & 0 \\ 0 & 0 & 0 & 1 \end{matrix}\right] $$

$$ rotXU = \left[\begin{matrix} cos(\theta) & 0 & 0 & sin(\theta) \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ -sin(\theta) & 0 & 0 & cos(\theta) \end{matrix}\right] $$

$$ rotYU = \left[\begin{matrix} 1 & 0 & 0 & 0 \\ 0 & cos(\theta) & 0 & -sin(\theta) \\ 0 & 0 & 1 & 0 \\ 0 & sin(\theta) & 0 & cos(\theta) \end{matrix}\right] $$

$$ rotZU = \left[\begin{matrix} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & cos(\theta) & -sin(\theta) \\ 0 & 0 & sin(\theta) & cos(\theta) \end{matrix}\right] $$

The source code can be found below as well as being bundled into the Jar file.

Transform4D.java - contains method for rotating a 4D vector

Transform4D.java

Point4D.java

Graph4D.java